About the Trip
In January of 2024, Leo and McKinley were joined with 3 others on the predecessor for this journey. This smaller, single day trip, consisted of a mere 6 Culver's, all owned by the same family. However, this trip may have been small, but it sprouted the idea of the ultimate tour of Every Culver's in Minnesota.

About McKinley
McKinley is a passionate lover of Culver's, and a frequenter of the local location. In his free time he can be found yapping about the news and playing hit computer game Antimatter Dimensions. His go-to order is Buffalo Chicken Tenders with Onion Rings and a Dr Pepper.

About Leo
Leo is currently an Assistant Manager at his local location and is an avid collector of Culver's merchandise. In his free time he can be found enjoying jazz music and playing Minecraft. His go-to order is Original Chicken Tenders with Fries and a Dr Pepper.
Here's a blog post written by Andy Rundquist detailing how to find the ideal route between all the Culver's locations:
Traveling Culvers Salesman
If you want to visit all the Culvers in Minnesota, how do you choose the order? You could start with the list and just go in the order you found this list. For Minnesota you can see the list here.
Here's a histogram showing how many hours it would take to drive to all the Culvers restaurants if you just randomly choose the order (they all assume you end at the same restaurant you started with).
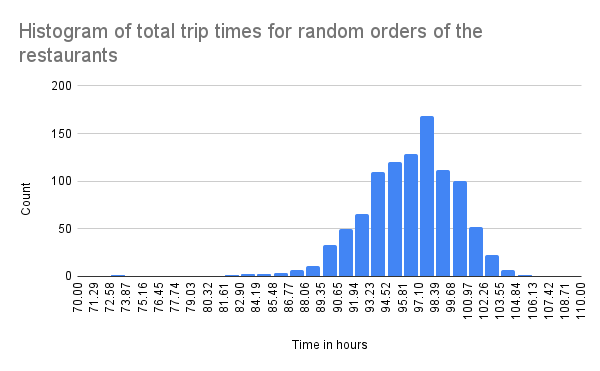
As you can see the typical average is something like four straight days of driving! That's not even counting all the time it would take you to order and eat a whole bunch of Concrete Mixers (or sleep, or call your parents, or . . .).
You can see that there are definitely some orders faster than others. How may different orders are there? Well, if there's 62 restaurants, then the number is 62! If you thought I was just saying the number in an excited voice, you'd be wrong. It's really 62 factorial, which is a huge number:
31 septenvigintillion 469 sexvigintillion 973 quinvigintillion 260 quattuorvigintillion 387 trevigintillion 937 duovigintillion 525 unvigintillion 653 vigintillion 122 novemdecillion 354 octodecillion 950 septendecillion 764 sexdecillion 88 quindecillion 12 quattuordecillion 280 tredecillion 797 duodecillion 258 undecillion 232 decillion 192 nonillion 163 octillion 168 septillion 247 sextillion 821 quintillion 107 quadrillion 200 trillion
(or 31,469,973,260,387,937,525,653,122,354,950,764,088,012,280,797,258,232,192,163,168,247,821,107,200,000,000,000,000). For the histogram above I just generated one thousand of those randomly, but the you still get the gist of the typical (random) choice. To calculate all of them, assuming it only takes a tenth of a second to calculate one of them (which is actually faster than my laptop but reasonable for a fast computer), it would take 10^50 times the lifetime of the universe to do it. So, that's a little out of the question if we want this trip to happen this summer.
So are we stuck with four straight days of driving? Of course not! Even looking at the histogram you can see a tiny little blue speck around 73 hours. That's only three days! But still, ugh, right? That one goes through all the Culvers in the order of their distance from the geographic center of Minnesota, which is actually the order you get with the link above from the Culvers web site. Really it just keeps spiraling around the center of Minnesota and it cuts a full ~24 hours off the typical random choice.
What I wanted to do was try to find the needle in the haystack of all possible orders that does the best, without having to calculate them all (I don't have even one lifetime of the universe to get this done). That's precisely what things called "Traveling Salesman" algorithms do. What I needed to do was calculate all the driving times among all pairs of Culvers (there's 1,891 pairs to consider!) and then use a traveling salesman algorithm to find the optimum path.
So how do you get the driving time between a pair of restaurants, and then how do you do that nearly two thousand times? The first part is easy if you just have a handful of pairs to do: you just ask something like Google Maps! But the second part (doing it 2000 times) is where you pause and wonder if you have the patience to do it. That's where scripting tools like python come in! This library, for example, will happily let you write a little script to check all two thousand pairs. Armed with all of those, you can then use Mathematica's FindShortestTour tool to find the best path.
And here it is!
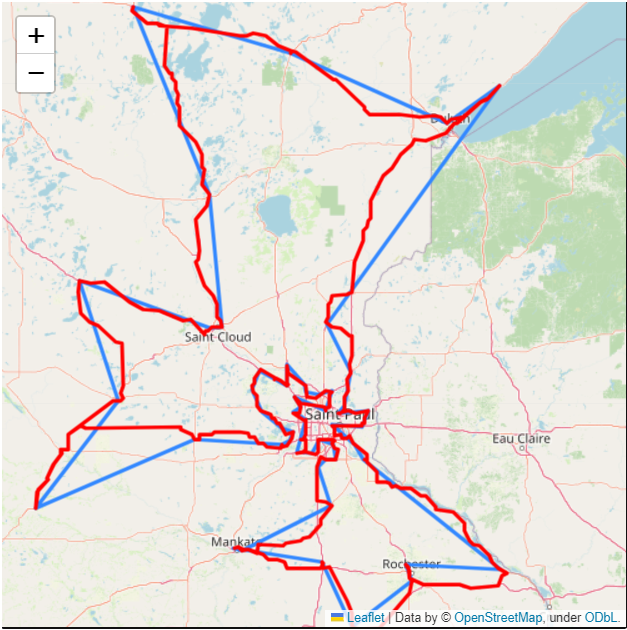
In blue you see all the restaurants connected in order by straight lines. In red you see the actual driving path that minimizes the whole trip.
Here's a zoom in on the twin cities:
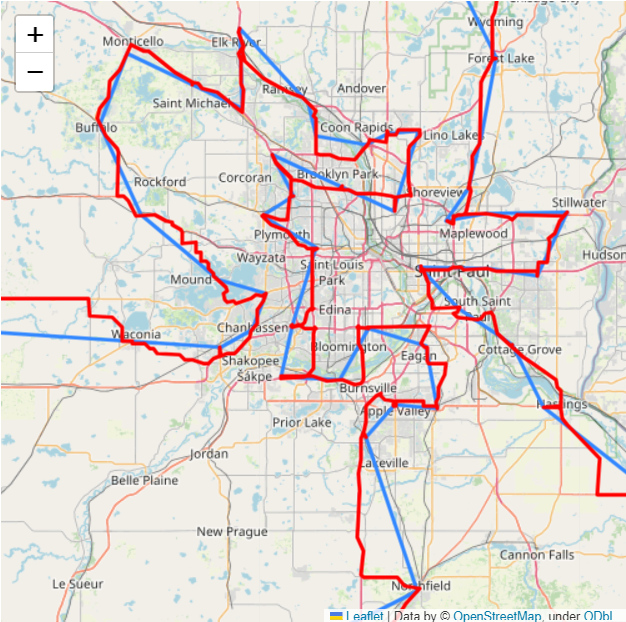
So how long? Only 33 hours of driving! Way better than the four full days it would have been with a random choice, that's for sure.
Of course, it's still a lot of Concrete Mixers :-)